Experimenting with Python implementation of Host Identity Protocol

Host Identity Protocol, or HIP, is a layer 3.5 solution and was initially designed to split the dual role of the IP address - locator and identifier. Using HIP protocol one can solve not only mobility problems but also establish authenticated secure channel between two communicating end-hosts. In this short article, we first introduce relevant background information. We then present some mathematical background related to Elliptic Curve (EC) Cryptography and Diffie-Hellman protocol based on EC. Finally, we demonstrate some micro benchmarking results for various cryptographic primitives and conclude the article with the results for the overall performance of HIP and IPSec, which we implemented in Linux userspace using Python language.
INTRODUCTIONSometimes it is easier to implement prototypes in userspace using high-level languages, such as Python or Java. In this document we attempt to describe our implementation effort related to Host Identity Protocol version 2. In the first part, we describe various security solutions, then we discuss some implementation details of the HIP protocol, and finally, in the last part of this work we discuss the performance of the HIP and IPSec protocols implemented using Python language.
BACKGROUNDIn this section we will describe basic background. First, we will discuss the problem of mobile Internet and introduce the Host Identity Protocol. We then move to the discussion of various security protocols. We will conclude the section with the discussion of Elliptic Curves and a variant of Diffie-Hellman algorithm, which uses EC cryptography (ECC).
Internet was designed initially so that the Internet Protocol (IP) address is playing dual role: it is the locator, so that the routers can find the recipient of a message, and it is an identifier, so that the upper layer protocols (such as TCP and UDP) can make bindings (for example, transport layer sockets use IP addresses and ports to make a connections). This becomes a problem when a networked device roams from one network to another, and so the IP address changes, leading to failures in upper layer connections. The other problem is establishment of the authenticated channel between the communicating parties. In practice, when making connections, long term identities of the parties are not verified. Of course, there are solutions such as SSL which can readily solve the problem at hand. However, SSL is suitable only for TCP connections and most of the time practical use cases include only secure web surfing and establishment of VPN tunnels. Host Identity Protocol on the other hand is more flexible: it allows peers to create authenticated secure channel on network layer, and so all upper layer protocols can benefit from such channel.
HIP [13] relies on the 4-way handshake to establish authenticated session. During the handshake, the peers authenticate each other using long-term public keys and derive session keys using Diffie-Hellman or Elliptic Curve (EC) Diffie-Hellman algorithms. To combat the denial-of-service attacks, HIP also introduces computational puzzles. HIP uses truncated hash of the public key as identifier in a form of IPv6 address and exposes this identifier to the upper layer protocols so that applications can make regular connections (for example, applications can open regular TCP or UDP socket connections). At the same time HIP uses regular IP addresses (both IPv4 and IPv6 are supported) for routing purposes. Thus, when the attachment of a host changes (and so does the IP address used for routing purposes), the identifier, which is exposed to the applications, stays the same. HIP uses special signaling routine to notify the corresponding peer about the change of locator. More information about HIP can be found in RFC 7401 [15].
There are a lot of solutions today which allow communicating parties to authenticate each other and establish secure channel. In this section, we will review some of the most widely used security protocols and discuss their application use cases. Here, we will also review some of the protocols which allow end-hosts to separate the dual role of the IP addresses.
Secure Shell protocol (SSH) is one security solution [5]. SSH is the application layer protocol which provides an encrypted channel for insecure networks. SSH was originally designed to provide secure remote command-line, login, and command execution. But in fact, any network service can be secured with SSH. Moreover, SSH provides means for creating VPN tunnels between the spatially separated networks: SSH is a great protocol for forwarding local traffic through remote server. However, the protocol will fail once the network device changes its attachment point in the network. IPSec [12] runs directly on top of the IP protocol and offers two various services: (i) it provides the so-called Authentication Header (AH), which is used only for authentication, and (ii) it provides Encapsulated Security Payload (ESP), which is an authentication plus payload encryption mechanism. To establish the security association (negotiate secret keys and algorithms) one can use IKE or IKEv2, ISAKMP or even preshared keys and set of negotiated beforehand security algorithms.
Internet Key Exchange protocol (IKE) [6] is a protocol used in IPSec to establish security association, just like HIP. Unlike HIP, however, IKE does not solve the dual role problem of the IP address. Secure socket layer (SSL) is an application layer solution to secure TCP connections. SSL was standardized in RFC 6101 [4]. And was designed to prevent eavesdropping, man-in-the-middle attacks, tampering and message forgery. In SSL the communicating hosts can authenticate each other with help of longer-term identities - public key certificates. Although, the solutions which we have listed above do solve security problems at various layers of the OSI [2] model, they are not designed to deal with node mobility. We, therefore, in the paragraphs that follow, list several protocols, which were designed specifically to support mobility and solve the dual role of an IP address.
Locator Identifier Separation Protocol (LISP) was specified in RFC 6830 [8]. In LISP identifiers and locators can be anything: IPv4 address, IPv6 address, Medium Access Control address, etc. Some of the advantages, besides separation of locator and identifier, include: address family traversal (IPv4 over IPv4, IPv4 over IPv6, IPv6 over IPv6, and even IPv6 over IPv4), mobility, and improved routing scalability.
Identifier/Locator Network Protocol (ILNP) was specified in several RFCs. It is worth to take a look at RFC 6740 [16], which contains protocol’s architectural description. The main advantage of ILNP is that it offers incremental deployment, and backwards compatibility with the IP protocol.
Mobile IP is another protocol to deal with node mobility. Despite that the protocol does not solve the separation of locator and identifier problem as such, we still refer it to this category, because it solves issues, which occur during node mobility. Thus, the protocol was originally designed to allow mobile users to move from one network to the other while maintaining permanent IP address. The protocol is specified in RFC 5944 [14] (for IPv4 protocol) and RFC 6275 [7] (for IPv6 protocol). The main disadvantage of the protocol, however, is its complexity.
We will now move on to the discussion of the limitations of the cryptography library which we have used when we were implementing the Host Identity Protocol using Python language.
The cryptography library (pycryptodome [3]), which we have used in our implementation, at the time of writing, did not support Diffie-Hellman (DH) and Elliptic Curve Diffie-Hellman (ECDH) algorithms. Thus, we have sat down and derived our own implementation of these algorithms. To make things a little bit clear, here we will mention some background (the reader can look at [17] for more information on EC cryptography) on Elliptic Curve Cryptography (ECC) and discuss the implementation details of ECDH.
Elliptic curves have the following form y²≡x³+ax+b mod p. For the curve to have at least one root the discriminant should be non-zero. In other words, δ=-16(4a³+27b² )≢ 0 mod p, where p is a large enough prime number. By defining a binary operation, which is an addition operation, we can make elliptic curve form an abelian group. Remember, abelian group has the following properties: (i) closure, meaning that if A,B ∈ E, then A+B ∈ E, (ii) associativity: ∀ A,B,C ∈ E follows that (A+B)+C=A+(B+C). (iii) existence of identity element I, such that A+I=I+A=A, (iv) existence of inverse: ∀A ∈ E A+A-1=A-1+A=I; (v) commutativity: ∀A,B ∈ E A+B=B+A. Finally, we should mention that there should exist an element G, such that multiple additions of such element with itself, kG, generates all other elements of the group. Such groups are called cyclic groups.
Let’s define O, a point at infinity, to be identity element, such that P+O=O+P=P,∀P ∈E. Also, we define P+(-P)=O, where -P=(x,-y). Next let’s suppose that P,Q ∈ E, where P=(x1,y1) and Q=(x2,y2). We can then distinguish the following three cases: (i) x1≠ x2 (in this case the line, which passes through the two given points, must intersect the curve somewhere at a third point R=(x3,y3), (ii) x1=x2 and y1=-y (in this case the line is vertical, and it does not pass through a third point on the curve); and finally (iii) x1=x2 and y1=y2 (in this case the line is tangent to a curve, but still crosses the curve at a third point R=(x3,y3)). Given case (ii), we can define a negative point as -R=(x,-y).
In the first case, line L passes through points P and Q. Using simple geometry, we can derive an equation of the line as follows: y=βx+ν, such that β=(y2-y1)(x2-x1)-1
Also, we can find ν as ν=y1-βx1=y2-βx2
In order to find the points that intersect the curve, we can substitute y=βx+ν into equation of an elliptic curve: (βx+ν)2=x3+ax+b
By rearranging the terms of the equation, we obtain: x³+ax+b-β² x²-2βνx-ν²=x³+(a-2βν)x-β² x²+b-ν²=0
But since the obtained equation has three roots, we have: (x-x1)(x-x2)(x-x3)=x³-(x3+x2+x1) x²+(x2 x3+x1 x3+x1 x2)x+x1 x2 x3
By noticing that the β²=x1+x2+x3, we have: x3=β²-x1-x2
Moreover, since P+Q=-R, we have: -y3=β(x3-x1)+y1 or y3=β(x1-x3)-y1
The second case is simple, by definition we have P-Q=O. And finally, we should mention that the third case is much like the first case, but with one difference - the line that passes through P and Q is tangent to the curve, because P=Q. By applying an implicit differentiation to an original function of an elliptic curve, we have: 2y ∂y/∂x=3x1²+a From this we can derive β as follows: ∂y/∂x=β=(3x1²+a)(2y1)-1 This expression allows us to derive the x3 as follows: x3=β²-2x1 Finally, just as in the first case, we have y3=β(x1-x3)-y1. Of course, all operations are done modulo prime p.
We now turn to discussion of ECDH protocol and some of the implementation details. We have used the parameters for the elliptic curve which are defined in RFC5903 [9]. ECDH proceeds in the following manner: Party A generates random number i, where the size of this random number is equal to the number of bytes that make up the prime number p (this is specified in the parameters set). Party B generates in a similar fashion number j. Both parties, using point on a curve G, which is also a generator (again specified in RFC5903), compute public keys: KA=iG and KB=jG. We have used well-known double and add algorithm [17] to efficiently compute the multiplication. Next parties exchange the public keys and derive a shared secret as follows S=jKA=iKB=ijG.To test the implementation we have used test vectors provided in previously mentioned RFC.
HARDWARE AND SOFTWAREFor hardware we have used the following setup. We have used single machine as initiator. The machine had dual core Intel Celeron processor, 16 GB of Random Access Memory (RAM) and 500 GB hard disk drive. The responder was less capable Raspberry PI microcontroller, but had quad core CPU each running at 1.0 GHz, 1 GB of RAM and a flash card for durable storage. For software we have used Ubuntu 18.04 on initiator, and Raspbian OS on the responder.
We have exposed our implementation of the HIPv2 protocol in GitHub repository. Interested readers can find it here [11].
EXPERIMENTAL EVALUATIONIn this section we will discuss the performance related issues of our HIPv2 implementation. We begin the discussion with the set of microbanchmarkings. Thus, we first evaluate the performance of ECDH and DH algorithms, then we switch to performance of RSA and ECDSA signature algorithms, we conclude the discussion with the performance evaluation of AES and HMAC algorithms. Afterwards, we present the results for the overall performance of the HIP implementation.
We start with the performance of puzzle computation. In Figure 1 we show the average duration of puzzle solution computation. Clearly, the hardness grows exponentially with the puzzle difficulty.
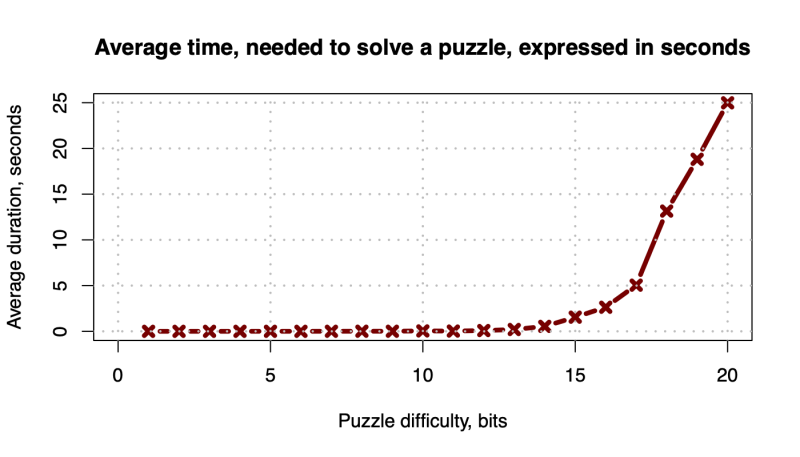
Figure 1: Average duration of puzzle solving
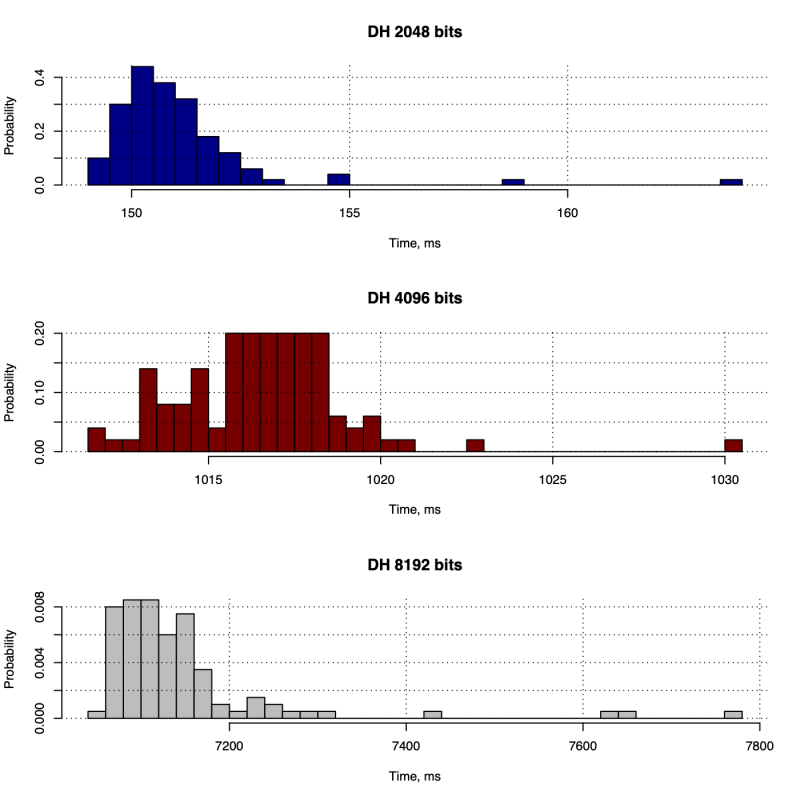
Figure 2: Diffie-Hellman key exchange duration (total)
To demonstrate the performance of ECHD and DH algorithms we have executed the key exchange algorithms 100 times for various groups. Thus, in Figure 2 we show the performance of DH and in Figure 3 we show the performance of ECDH for various curve parameters. To understand how two are related in Table 1 we show the sizes of various keys and how they are related to symmetric keys.
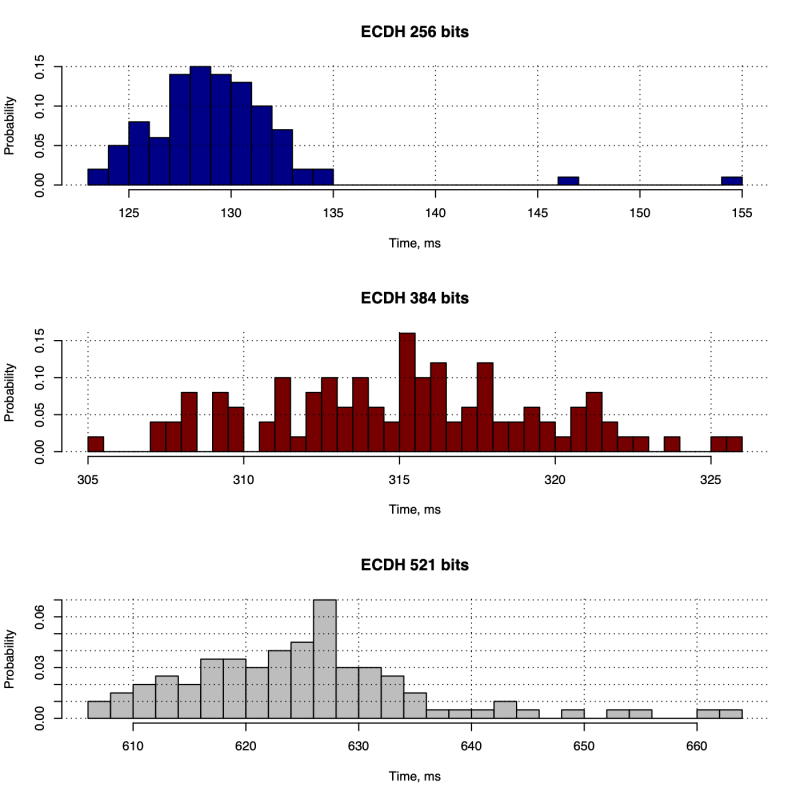
Figure 3: Elliptic Curve Diffie-Hellman key exchange duration (total)
| Symmetric key size, bits | DH keys, bits | ECDH keys, bits |
| 80 | 1024 | 160 |
| 112 | 2048 | 160 |
| 128 | 3072 | 256 |
| 192 | 7680 | 384 |
| 256 | 15360 | 521 |
Table 1: Security strength of keys
Obviously, ECDH shows far better performance than regular DH algorithm. This performance improvement is largely due to reduced key sizes. Next, we have measured the computational performance of other cryptographic primitives. Thus, in Table 2 we show summary statistics for all the operations we have completed.
| Operation | Mean time, ms | Median time, ms | Standard deviation, ms |
| RSA (2048 bits, SHA-256) signing | 2.099 | 2.094 | 0.026 |
| RSA (2048 bits, SHA-256) verification | 0.591 | 0.589 | 0.008 |
| ECDSA (secp384r1, SHA-384) signing | 1.379 | 1.374 | 0.042 |
| ECDSA (secp384r1, SHA-384) verification | 3.008 | 3.006 | 0.016 |
| AES-256 encryption | 0.036 | 0.031 | 0.027 |
| AES-256 descryption/td> | 0.032 | 0.029 | 0.017 |
| HMAC (SHA-256) | 0.057 | 0.054 | 0.018 |
Table 2: Performance of cryptographic primitives
We have performed 100 rounds of measurements for each cryptographic primitive. The size of the data for all operations was selected to be 1500 bytes. We have run the HIPv2 BEX for 20 times and measured the total packet processing time (we have combined packet processing time for initiator and responder). In Figure 4 we show the boxplots for the packet processing duration. To run the tests, we have used the following configuration: for signatures we have used RSA with 2048 bits long modulus, SHA-256 for HMAC and hashing, ECDH with NIST521 curve, AES-256 for encryption and 16 bits for puzzle difficulty. We have noticed that processing R1 packet consumes considerable amount of time on responder. Since our implementation was lacking pre-creation of R1 packets, such lengthy packet processing time was expected. We have also measured the overall duration of the HIPv2 base exchange (BEX). In Figure 4 we show the time required to process HIP packets and in Figure 5 we demonstrate distribution of HIP BEX durations.
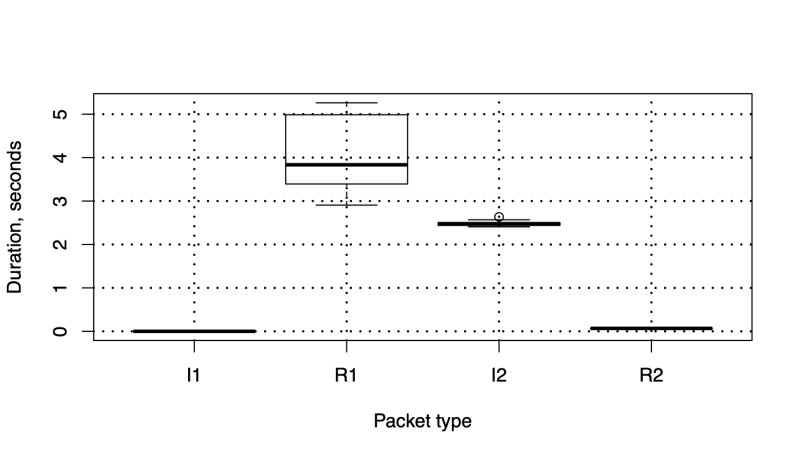
Figure 4: Packets’ processing time
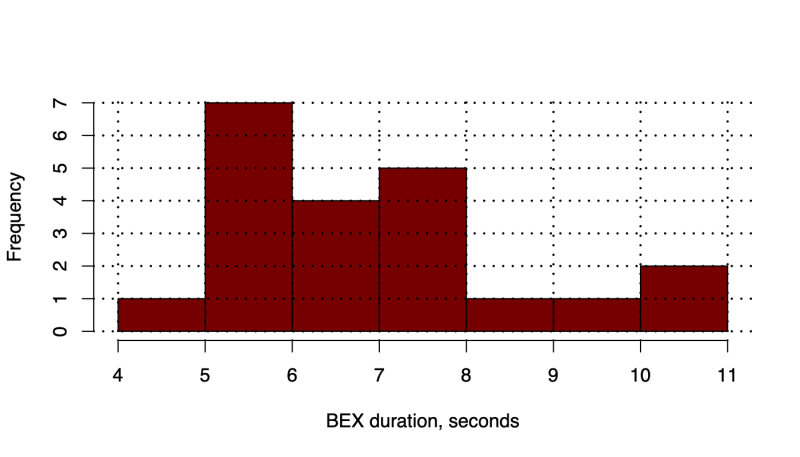
Figure 5: Duration of HIPv2 BEX
Clearly, implementing cryptographic protocols in userspace using high-level languages, such as Python, is not the best choice: the performance of such implementations is somewhat unacceptable for production servers and it is better to implement the security solutions for overloaded servers using lower-level languages, such as C or C++. On the other side, Python implementation is more suitable for study and experimental purposes. Finally, we have measured throughput for TCP connections over IPSec tunnel and plain TCP. We have used iperf [1] tool to measure throughput. Clearly, with our implementation we were able to achieve throughput slightly 25 times less, than throughput, which we have obtained for plain TCP connections (Figure 6). Such result was expected for Python implementations of security protocols. For example, we have observed similar behavior with our Python implementation of VPN solution in one of our previous studies [10].
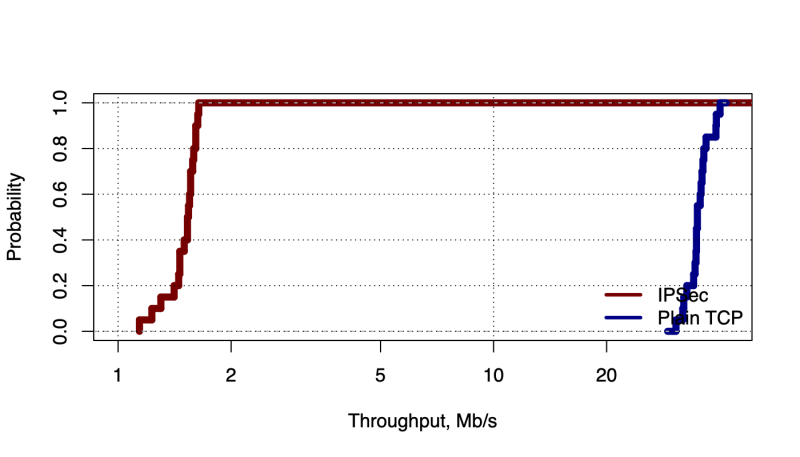
Figure 6: Obtained throughput for TCP over IPSec and plain TCP connections
CONCLUSIONSIn this short article we have discussed the implementation details of Host Identity Protocol (HIP), which is a layer 3.5 security solution aiming at separation of dual role of an IP address. HIP protocol not only solves the problem of separation of roles of the IP addresses, but can also be a secure mobility solution. There are many applications of HIP in modern networks - from establishing a secure channel between stationary network entities, to securing mobile users. We have created a minimal Python-based implementation of HIP and experimented with it: (i) we have made several microbanchmarkings, and (ii) we completed several rounds of stress tests of the solution. We have also implemented Encapsulated Secure Payload (ESP) for IPSec and measured overall performance by performing several rounds of bandwidth measurements using iperf tool. We hope that the implementation of HIP will be useful and interesting for other people. For that reason, we have exposed it in public repository [11].
REFERENCES[1] iPerf - The ultimate speed test tool for TCP, UDP and SCTP. https://iperf.fr/, 2021.
[2] OSI model. https://en.wikipedia.org/wiki/OSI model, 2021.
[3] PyCryptodome. https://pycryptodome.readthedocs.io/en/latest/, 2021.
[4] A. Freier, P. Karlton, P. Kocher. The Secure Sockets Layer (SSL) Protocol Version 3.0. https://datatracker.ietf.org/doc/html/rfc6101, 2011.
[5] D. J. Barrett, R. E. Silverman, and R. G. Byrnes. SSH, the Secure Shell: The Definitive Guide. O’Reilly Media, Inc., 2005.
[6] C. Kaufman, P. Hoffman, Y. Nir, P. Eronen. Internet Key Exchange Protocol Version 2 (IKEv2). https://datatracker.ietf.org/doc/html/rfc5996, 2010.
[7] J. A. C. Perkins, D. Johnson. Mobility Support in IPv6. https://datatracker.ietf.org/doc/html/rfc6275
[8] D. Farinacci, V. Fuller, D. Meyer, D. Lewis. The Locator/ID Separation Protocol (LISP). https://datatracker.ietf.org/doc/html/rfc6830, 2013.
[9] D. Fu and J. Solinas. Elliptic Curve Groups modulo a Prime (ECP Groups) for IKE and IKEv2. https://datatracker.ietf.org/doc/html/ RFC5903, 2010.
[10] D. Kuptsov. Bypassing Deep Packet Inspection: Tunneling Traffic Over TLS VPN. https://www.linuxjournal.com/content/bypassing-deep-packet-inspection-tunneling-traffic-over-tls-vpn, 2021.
[11] D. Kuptsov. CuteHIP: Python implementation of Host Identity Protocol. https://github.com/dmitriykuptsov/cutehip, 2021.
[12] N. Doraswamy and D. Harkins. IPSec: The New Security Standard for the Internet, Intranets, and Virtual Private Networks. Prentice Hall PTR, USA, 1999.
[13] A. Gurtov. Host Identity Protocol (HIP): Towards the Secure Mobile Internet. Wiley Series on Communications Networking and Distributed Systems. Wiley, 2008.
[14] C. Perkins. IP Mobility Support for IPv4, Revised. https://datatracker.ietf.org/doc/html/rfc5944
[15] R. Moskowitz, T. Heer, P. Jokela, T. Henderson. Host Identity Protocol Version 2 (HIPv2). https://datatracker.ietf.org/doc/html/rfc7401, 2015.
[16] RJ Atkinson, SN Bhatti. Identifier-Locator Network Protocol (ILNP) Architectural Description. https://datatracker.ietf.org/doc/html/rfc6740, 2012.
[17] D. Stinson. Cryptography: Theory and Practice, Second Edition. CRC/C&H, 2nd edition, 2002.






